Dictionary Learning Theory
Can we learn a dictionary from training samples with performance guarantees?
Dictionary Learning Theory
Can we robustly identify an underlying ideal dictionary D, given a set Y = [y1 ... yN] of training data available in limited quantity and/or corrupted by noise or outliers?
This has been investigated under a theoretical framework based on L1 minimization, minD,X ||X||1 s.t. D∈D, Y=DX, which is non-convex in this context.
The robustness of the approach to non-sparse outliers and limited training data has been proved under certain probabilistic scenarios.
Achievements
The local correctness of the approach has been proved under certain probabilistic scenarios (Bernoulli-Gaussian coefficients X) for square dictionaries.
- Robustness to the presence of outliers (non-sparse training samples) is proved assuming the ground truth dictionary is sufficiently incoherent;
- Robustness to the limited amount of training data is proved provided the number N of training samples exceed N ≥CKlogK where K is the number of atoms of the dictionary and the constant C depends on a parameter of the Bernoulli-Gaussian distribution which drives the sparsity of the training set.
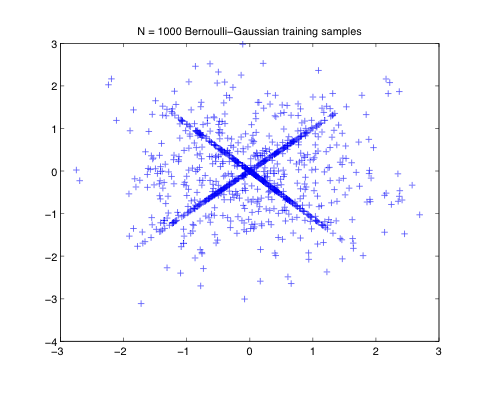 | 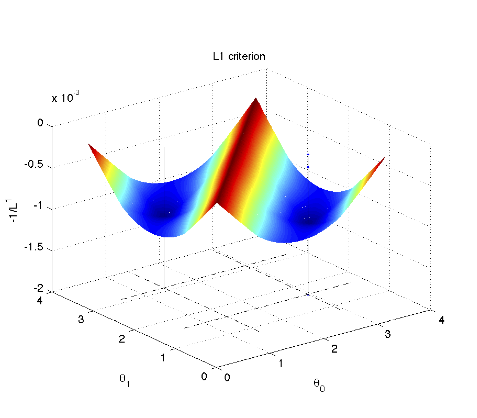 |
| Bernoulli-Gaussian training samples include boths sparse vectors (aligned on low dimensional subspaces) and outliers. | With high probability, local minima of the L1 cost function are global minima identifying the ground truth dictionary |
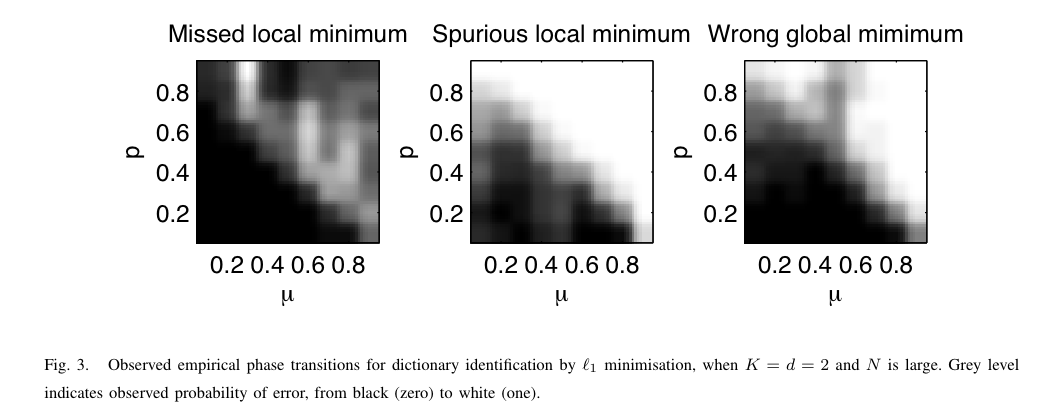 | |
The minima of the L1 criterion identify the dictionary with high probability, for dictionaries with low enough coherence μ / small enough Bernoulli-Gaussian parameter p (p drives the sparsity level and the proportion of non-sparse outliers). | |
More details
